This notebook shows how physical properties like the isothermal compressibility can be calculated from accurate thermodynamic potentials (in this case, Fiestel’s Gibbs free energy function for ice, used in oceanographic modeling). It also introduces function definition in Maxima.
- Download and install the Euler Math Toolbox.
- Cut and paste the code for notebook3.3 below into a plain text file, and save it as “notebook3.3.en”.
- Cut and paste the code for Gice into a plain text file, and save it as “Gice.e”. This file must be placed in the same directory as notebook3.3.en.
- Double-click notebook3.3.en. It should open up in the Toolbox.
All of the notebooks in this series are specifically keyed to Atkins’ Physical Chemistry, 8th edition. Italics mark the items students had to fill in themselves.
--------------------------------------------------notebook 3.3 code begins------------------------------------------
Notebook 3.3 Calculating Physical Properties from Thermodynamic Potentials
%
% In this notebook, we'll use thermodynamic potentials to predict material properties.
% In particular, we'll use an empirical Gibbs free energy function for ice to show how
% properties like density, energy, and entropy vary with temperature and pressure.
%
% REFERENCES
% 1. Fiestel, R., Wagner, W., Tchijov, V., Guder, C.,
% "Numerical implementation and oceanographic application of the Gibbs
% potential of ice", Ocean Science, 1, 29-38, 2005.
% 2. Fiestel, R., Wright, D. G., Miyagawa, K., Harvey, A. H, Hruby, A. H.,
% Jackett, D. R., McDougall, T. J., Wagner, W., "Mutually consistent
% thermodynamic potentials for fluid water, ice, and seawater: a new
% standard for oceanography", Ocean Science, 4, 275-291, 2008.
%
% BACKGROUND
% We can calculate many material properties as first and second derivatives
% of the Gibbs free energy (see Section 3.9 in Atkins 8e).
% We've already seen how functions can be defined in Euler. In this notebook,
% we'll define functions in Maxima using the ":=" operator. For example, to
% define a function that calculates the area of a circle from its radius,
% we can type
%
>: area(r) := %pi*r^2
2
area(r) := %pi r
%
% The area of a circle with a radius of 2 m can be calculated as
>: area(2)
4 %pi
% or
>: area(r), r=2
4 %pi
%
% ...both mean the same thing, and give the same result.
%
% We've already seen that we can calculate derivatives like dA/dr
% with the diff() function:
%
>: diff(area(r),r)
2 %pi r
%
% We can calculate second derivatives as well by repeating the differentiation
%
>: diff(diff(area(r),r), r)
2 %pi
%
% but there's an easier way. Maxima lets you specify the order of the derivative
% as a third argument to diff.
% For the second derivative of area with respect to r, we can type
%
>: diff(area(r),r,2)
2 %pi
% --------------------------------------------------------------------------------------------------------------------------------------------------------------
% In the space below, calculate the surface area of a sphere from its volume.
% The volume of a sphere is (4/3) pi r^3, and the surface area of the sphere is
% dV/dr.
%
>: V(r) := (4/3)*%pi*r^3
4 3
V(r) := - %pi r
3
>: surfacearea : diff(V(r),r)
2
4 %pi r
%
% The line below loads the thermodynamic potential from Reference
% 1 into Maxima from an external file ("Gice.e"). The Maxima function
% Gice(T,P) computes the Gibbs free energy of one kilogram of ice
% (in J/kg) at a temperature of T (in K) and a pressure of P (in
% Pa).
%
>load("Gice")
%
% We can have Maxima print back the Gice(T,P) function for us:
>: Gice(T,P)
2
273.16 (- 65.22370501477501 (1.7162371555667344E-4 T
+ atan2(0.051046477118412, 0.0036608581051398 T + 0.037153909034639)
(0.0036608581051398 T + 0.037153909034639)
+ atan2(0.051046477118412, 0.037153909034639 - 0.0036608581051398 T)
(0.037153909034639 - 0.0036608581051398 T)
2
+ 0.025523238559206 log((0.0036608581051398 T + 0.037153909034639)
+ 0.0026057428262006) + 0.025523238559206
2
log((0.037153909034639 - 0.0036608581051398 T) + 0.0026057428262006)
+ 0.21205793408363) - (- 2.7329787774916599E-11
2
(0.0016349032219038 P - 165.6565689594)
+ 5.0905901194652602E-5 (0.0016349032219038 P - 165.6565689594)
2
- 80.98785064626451) (1.9417364295872538E-5 T
+ atan2(0.34331589201784, 0.0036608581051398 T + 0.34509582956282)
(0.0036608581051398 T + 0.34509582956282)
+ atan2(0.34331589201784, 0.34509582956282 - 0.0036608581051398 T)
(0.34509582956282 - 0.0036608581051398 T)
2
+ 0.17165794600892 log((0.0036608581051398 T + 0.34509582956282)
+ 0.11786580171201) + 0.17165794600892
2
log((0.34509582956282 - 0.0036608581051398 T) + 0.11786580171201)
- 0.045958113581803) + (2.3961751351811602E-11
2
(0.0016349032219038 P - 165.6565689594)
- 5.7552976563435302E-5 (0.0016349032219038 P - 165.6565689594)
2
- 75.8695106343435) (- 1.951803454312407E-5 T
2
+ (log((0.0036608581051398 T + 0.34509582956282) + 0.11786580171201)
(0.0036608581051398 T + 0.34509582956282))/2
2
+ (log((0.34509582956282 - 0.0036608581051398 T) + 0.11786580171201)
(0.34509582956282 - 0.0036608581051398 T))/2
- 0.34331589201784 atan2(0.34331589201784,
0.0036608581051398 T + 0.34509582956282)
- 0.34331589201784 atan2(0.34331589201784,
0.34509582956282 - 0.0036608581051398 T) + 1.034399513744271)
2
+ 45.951447199735 (- 1.2491541583149561E-4 T
2
+ (log((0.0036608581051398 T + 0.037153909034639) + 0.0026057428262006)
(0.0036608581051398 T + 0.037153909034639))/2
2
+ (log((0.037153909034639 - 0.0036608581051398 T) + 0.0026057428262006)
(0.037153909034639 - 0.0036608581051398 T))/2
- 0.051046477118412 atan2(0.051046477118412,
0.0036608581051398 T + 0.037153909034639)
- 0.051046477118412 atan2(0.051046477118412,
0.037153909034639 - 0.0036608581051398 T) + 0.30140605416073))
+ 3333.18160308627 T - 5.7859365867952202E-22
4
(0.0016349032219038 P - 165.6565689594)
3
+ 3.40692612753936E-15 (0.0016349032219038 P - 165.6565689594)
2
- 1.89952376891314E-8 (0.0016349032219038 P - 165.6565689594)
+ 0.65502999780479 (0.0016349032219038 P - 165.6565689594) - 632578.704355102
%
% We can use this function to compute (and graph) almost all of
% the major state functions for ice. For example, (dG/dP)_T = V,
% so the volume of one kilogram of ice can be calculated using the
% line below.
%
% Notice that we calculate (dG/dP)_T symbolically with diff(), and
% then evaluate it at t,p using at(). In English, the following
% line says, "V(t,p) is the value of dG/dP at temperature t and
% pressure p".
%
%
>: V(t,p) := at(diff(Gice(T,P), P), [T=t, P=p])
V(t, p) := at(diff(Gice(T, P), P), [T = t, P = p])
%
% At 263.15 K and 10101325 Pascals, the volume of one kilogram of ice (in
% cubic meters) is
>: V(263.15,10101325)
0.0010878711964292
%
% Let's plot the volume of 1 kilogram of ice as a function of temperature
% from 250 K to 280 K, at a constant pressure of 1 atm.
%
% First, we define lists of temperatures and volumes to plot. It's
% going to be easier if the temperature list can be read by both
% Maxima and Euler. Notice that
%
% >Temperature = 250:280 would define the array ONLY in Euler,
%%>Temperature ::= 250:280 defines the array in BOTH Maxima and
% Euler.
%
% If the ::= operator doesn't work, you're using an old version
% of Euler. Upgrade.
> Temperature ::=250:280;
%
% Now we use the Maxima function V(t,p) to make a list of volumes
% in Euler. Recall that the mxmeval function sends a command (in
% double quotes) from Euler to Maxima.
> Volume = mxmeval("V(Temperature,p)", p=101325);
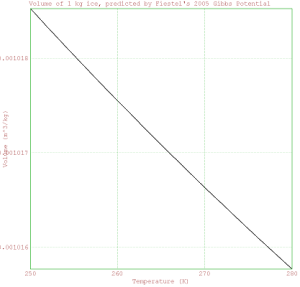
> plot2d(Temperature,Volume);
> xlabel("Temperature (K)");
> ylabel("Volume (m^3/kg)");
> title("Volume of 1 kg ice, predicted by Fiestel's 2005 Gibbs Potential");
> insimg;
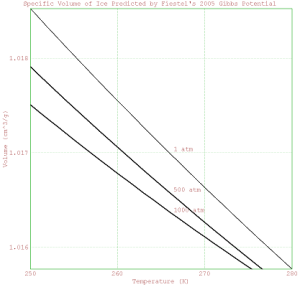
 >Volume = mxmeval("V(Temperature,p)", p=101325)*(1/1e-6)*(1/1000);
>plot2d(Temperature, Volume);
>label("1 atm",266,mean(Volume));
>Volume = mxmeval("V(Temperature,p)", p=500*101325)*(1/1e-6)*(1/1000);
>plot2d(Temperature, Volume, add=1, thickness=2);
>label("500 atm",266,mean(Volume));
>Volume = mxmeval("V(Temperature,p)", p=1000*101325)*(1/1e-6)*(1/1000);
>plot2d(Temperature, Volume, add=1, thickness=2);
>label("1000 atm",266,mean(Volume));
> xlabel("Temperature (K)");
> ylabel("Volume (cm^3/g)");
> title("Specific Volume of Ice Predicted by Fiestel's 2005 Gibbs Potential");
>insimg;
>Volume = mxmeval("V(Temperature,p)", p=101325)*(1/1e-6)*(1/1000);
>plot2d(Temperature, Volume);
>label("1 atm",266,mean(Volume));
>Volume = mxmeval("V(Temperature,p)", p=500*101325)*(1/1e-6)*(1/1000);
>plot2d(Temperature, Volume, add=1, thickness=2);
>label("500 atm",266,mean(Volume));
>Volume = mxmeval("V(Temperature,p)", p=1000*101325)*(1/1e-6)*(1/1000);
>plot2d(Temperature, Volume, add=1, thickness=2);
>label("1000 atm",266,mean(Volume));
> xlabel("Temperature (K)");
> ylabel("Volume (cm^3/g)");
> title("Specific Volume of Ice Predicted by Fiestel's 2005 Gibbs Potential");
>insimg;
 % ----------------------------------------------------------
%%In the space below, define a function that calculates the coefficient
% of isothermal compressibility
%
% kappa_T = -(1/V)(dV/dP)_T
%
% for ice as a function of temperature and pressure. Call your function
% to calculate the isothermal compressibility of ice at the triple
% point; under those conditions, kappa_T is about 1.18 x 10^-10
% Pa^-1.
%
%
>: kappaT(t,p) := at(-(1/V(T,P))*diff(V(T,P),P),[T=t,P=p]);
1
kappaT(t, p) := at((- -------) diff(V(T, P), P), [T = t, P = p])
V(T, P)
>: kappaT(273.16,611.657)
1.1791917359556073E-10
% --------------------------------------------------------------
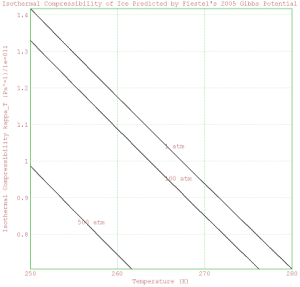
%%In the space below, plot the isothermal compressibility for ice
% predicted for temperatures from 250 K to 280 K, at pressures of
% 1, 100, and 500 atm. Scale the y-axis of the plot so it is easy
% to read, and label each individual curve on your plot.
%
>scalefactor=10^floor(log(mxmeval("kappaT(t,p)",t=mean(Temperature),p=101325))/log(10))
1e-011
>kappaTvalues = mxmeval("kappaT(t,p)",t=Temperature,p=101325)/scalefactor;
>plot2d(Temperature,kappaTvalues);
>xlabel("Temperature (K)");
>ylabel("Isothermal Compressibility kappa_T (Pa^-1)/" | scalefactor);
>title("Isothermal Compressibility of Ice Predicted by Fiestel's 2005 Gibbs Potential");
>label("1 atm",mean(Temperature),mean(kappaTvalues));
>kappaTvalues = mxmeval("kappaT(t,p)",t=Temperature,p=100*101325)/scalefactor;
>plot2d(Temperature,kappaTvalues,add=1);
>label("100 atm",mean(Temperature),mean(kappaTvalues));
>kappaTvalues = mxmeval("kappaT(t,p)",t=Temperature,p=500*101325)/scalefactor;
>plot2d(Temperature,kappaTvalues,add=1);
>label("500 atm",255,0.85);
>insimg;
% ----------------------------------------------------------
%%In the space below, define a function that calculates the coefficient
% of isothermal compressibility
%
% kappa_T = -(1/V)(dV/dP)_T
%
% for ice as a function of temperature and pressure. Call your function
% to calculate the isothermal compressibility of ice at the triple
% point; under those conditions, kappa_T is about 1.18 x 10^-10
% Pa^-1.
%
%
>: kappaT(t,p) := at(-(1/V(T,P))*diff(V(T,P),P),[T=t,P=p]);
1
kappaT(t, p) := at((- -------) diff(V(T, P), P), [T = t, P = p])
V(T, P)
>: kappaT(273.16,611.657)
1.1791917359556073E-10
% --------------------------------------------------------------
%%In the space below, plot the isothermal compressibility for ice
% predicted for temperatures from 250 K to 280 K, at pressures of
% 1, 100, and 500 atm. Scale the y-axis of the plot so it is easy
% to read, and label each individual curve on your plot.
%
>scalefactor=10^floor(log(mxmeval("kappaT(t,p)",t=mean(Temperature),p=101325))/log(10))
1e-011
>kappaTvalues = mxmeval("kappaT(t,p)",t=Temperature,p=101325)/scalefactor;
>plot2d(Temperature,kappaTvalues);
>xlabel("Temperature (K)");
>ylabel("Isothermal Compressibility kappa_T (Pa^-1)/" | scalefactor);
>title("Isothermal Compressibility of Ice Predicted by Fiestel's 2005 Gibbs Potential");
>label("1 atm",mean(Temperature),mean(kappaTvalues));
>kappaTvalues = mxmeval("kappaT(t,p)",t=Temperature,p=100*101325)/scalefactor;
>plot2d(Temperature,kappaTvalues,add=1);
>label("100 atm",mean(Temperature),mean(kappaTvalues));
>kappaTvalues = mxmeval("kappaT(t,p)",t=Temperature,p=500*101325)/scalefactor;
>plot2d(Temperature,kappaTvalues,add=1);
>label("500 atm",255,0.85);
>insimg;
 -------------------------------notebook 3.3 code ends------------------------------------------------------------------
-------------------------------Gice code begins------------------------------------------------------------------------------
:Gice(T,P) := block([g0: [-632578.704355102, 0.655029997804786, -1.89952376891314e-8,
3.40692612753936e-15,-5.78593658679522e-22], t: [3.71539090346389e-2 +
5.10464771184122e-2*%i, 0.345095829562823 + 0.343315892017841*%i], r:
[45.951447199735 + 65.223705014775*%i, 0.0 + 0.0*%i],r2: [-75.8695106343435
-80.9878506462645*%i, -5.75529765634353e-5 + 5.09059011946526e-5*%i,
2.39617513518116e-11 -2.73297877749166e-11*%i], Tt: 273.160, Pt: 611.657, p0:
165.6565689594, Pr: P/Pt, Tr: T/Tt, sigma0: -3333.18160308627], r[2]: sum(r2[k+1]*(P/Pt-
p0)^k,k,0,2), -sigma0*T + sum(g0[k+1]*(P/Pt-p0)^k,k,0,4)+Tt*realpart(sum(r[k]*((t[k]-T
/Tt)*log(t[k]-T/Tt) + (t[k]+T/Tt)*log(t[k]+T/Tt) - 2*t[k]*log(t[k])-(T/Tt)^2/t[k]),k,1,2)))$
%
function atan2(y,x) := atan(y/x)
------------------------------Gice code ends--------------------------------------------------------------------------------
-------------------------------notebook 3.3 code ends------------------------------------------------------------------
-------------------------------Gice code begins------------------------------------------------------------------------------
:Gice(T,P) := block([g0: [-632578.704355102, 0.655029997804786, -1.89952376891314e-8,
3.40692612753936e-15,-5.78593658679522e-22], t: [3.71539090346389e-2 +
5.10464771184122e-2*%i, 0.345095829562823 + 0.343315892017841*%i], r:
[45.951447199735 + 65.223705014775*%i, 0.0 + 0.0*%i],r2: [-75.8695106343435
-80.9878506462645*%i, -5.75529765634353e-5 + 5.09059011946526e-5*%i,
2.39617513518116e-11 -2.73297877749166e-11*%i], Tt: 273.160, Pt: 611.657, p0:
165.6565689594, Pr: P/Pt, Tr: T/Tt, sigma0: -3333.18160308627], r[2]: sum(r2[k+1]*(P/Pt-
p0)^k,k,0,2), -sigma0*T + sum(g0[k+1]*(P/Pt-p0)^k,k,0,4)+Tt*realpart(sum(r[k]*((t[k]-T
/Tt)*log(t[k]-T/Tt) + (t[k]+T/Tt)*log(t[k]+T/Tt) - 2*t[k]*log(t[k])-(T/Tt)^2/t[k]),k,1,2)))$
%
function atan2(y,x) := atan(y/x)
------------------------------Gice code ends--------------------------------------------------------------------------------
 Molecular Sieve is the work blog of
Molecular Sieve is the work blog of